【C言語】ビット演算

ビットとは、なにか。

プログラミングを始めようとする時、この「ビット」の理解ができないと、必ずつまづきます。

特に、WindowsやMac、Linux、クラウドサーバー等はメモリがたくさんあるため、ビット単位でメモリを管理するようなことはないですが、マイコンCPUを扱う場合などはメモリが極端に少ないため（最近はメガ単位のメモリを搭載したCPUも増えましたけどね）、ビット単位でデータを扱うケースも少なくはありません。

また、トランシーバーでデータ転送を扱う際などにも、極力小さいデータサイズで通信できるように、ビット演算でのデータ構成を使うことが多いです。

---

ビットとは

ビットとは、デジタルの世界での情報を表す最小の単位をいいます。

「binary digit」の略で、業界では「bit」と表現されます。

このビットの集まりを「ビット列」といい、あらゆるコンピューターはこの「ビット」を解析して動いています。

この「ビット」は、「0」と「1」だけで構成され、コンピュータ等の電子回路上では電圧のオン（電圧がかかっている状態）とオフ（電圧がかかっていない状態）の２種類の状態をデジタルで表現したものです。

また、ビットは、8つのビット列が揃うと「バイト」という単位で表現されます。

1バイト = 8ビット
2バイトデータの場合は、16ビット
3バイトデータの場合は、24ビット
4バイトデータの場合は、32ビット

1バイト = 8ビット

4バイトのデータは、32ビットということになります。

「１バイト」のデータは基本的には１文字の半角文字を表すことができるサイズで、一般的にもよく知られている単位です。

たとえば、1バイト文字、半角での「A」をビットに置き換えると以下のようになる。

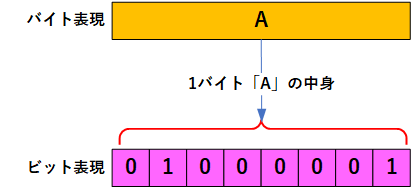
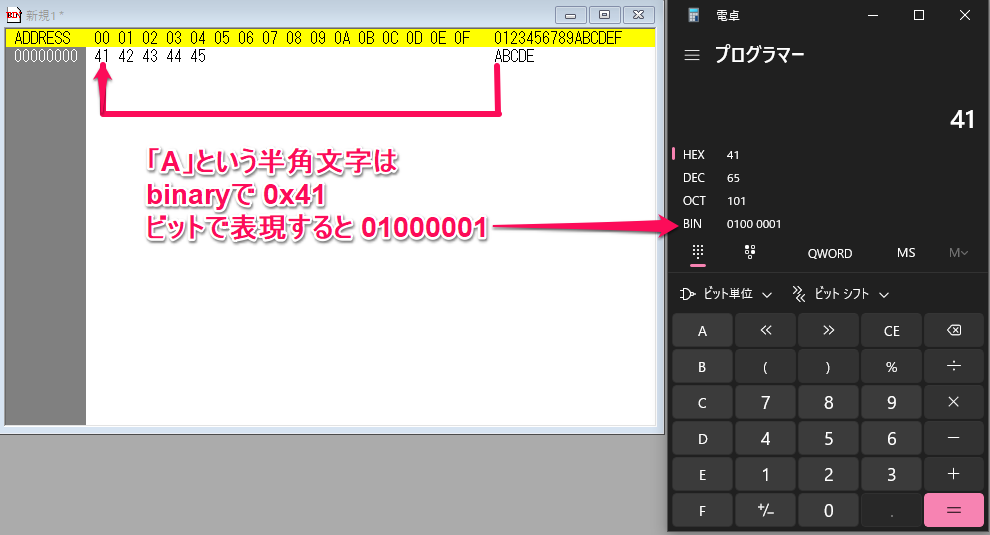
何故「A」が「0x41」になるのかというのは、「文字コード」をいうものが存在するためであって、文字コードについては別のページで説明します

上図のように、半角での「ABCDE」は、５バイトで表現でき、５×８＝40ビットで表現できるデータとなる。

このように、ビットの集合体（ビット列）で世の中のデジタル技術は成り立っています。

---

ビットの特徴

ビットは、基本的に「数値」であり、その「数値」が「文字コード」により、アプリケーションで「文字」として画面などに表示しています。

その数値は、「1バイト」増えるたびに値も「1増える」という特徴があります。

00000001　は、数値で「1」
ここに「1ビット」増やすと
00000010　となり、数値で「2」となる。

ビットは、必ず一番小さい桁のビット（一番右）から「1」ずつ増えていきます。既に一番小さい桁に「1」が入っているときは、次の桁へ繰り上がります。

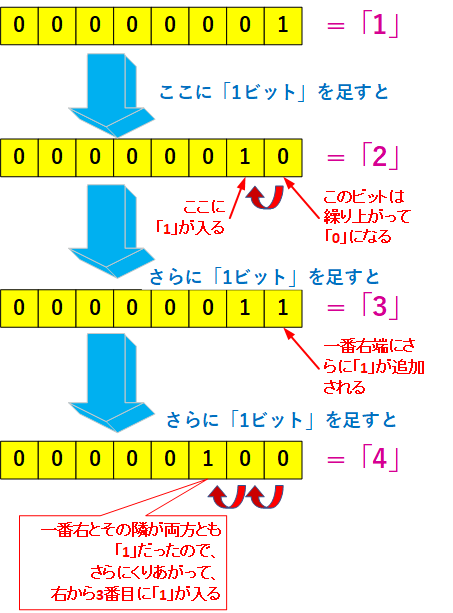
小学校で習うひっ算の繰り上がりみたいですね。

このようにして、コンピューター内での演算は、ビット単位で計算が行われています。

---

ビット演算子

ビット演算を知ることができると、とても便利なものです。

ビット演算の種類は大きく分けて２種類が存在します。演算を行う上で、色々な記号が用いられますが、このページでは、Ｃ言語で使うことを前提に説明します。

1. 論理演算

論理演算は、論理値のもと「真」「偽」を求める演算です。C言語では「if」文などによく使われますね。

1-1. 論理積（AND）

論理積は、２つの条件の真偽を判定する演算で、2つのビットが両方とも「1」の場合に「真(true)=1」を返し、それ以外の場合は「偽(false)=0」を返します。

論理積の記号：&&
【例】A = 1、B = 1
　　　A && B = 真（true:1）　　// AとBが同じかどうか
【例】A = 10、B = 11
　　　A && B = 偽（false:0）　 // AとBが同じかどうか
【例】A = 1、B = 2、C = 3、C = 4
　　　((A+B) && (C+D)) = 偽（false:0）　// (A+B)の答えと(C+D)の答えが同じかどうか

((A+B) && (C+D))　を例にすると

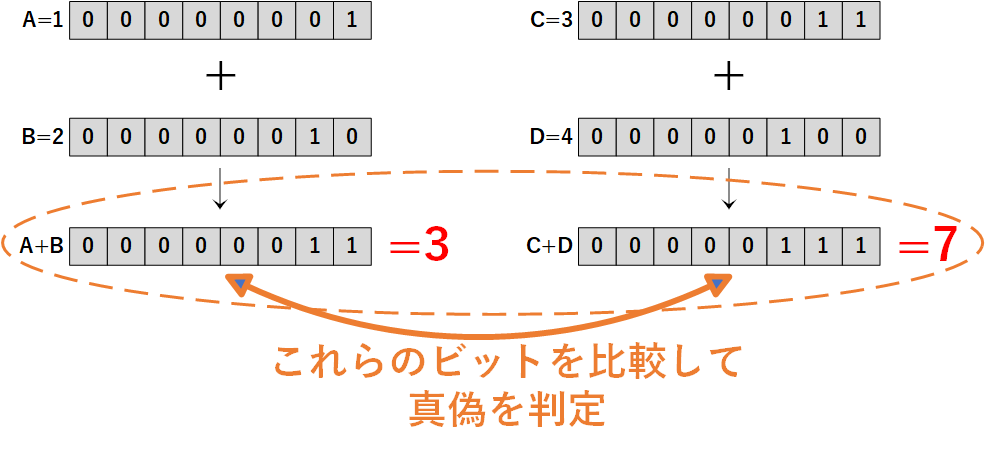
こういった論理積の演算を、C言語の「if」文に入れた場合、

int A = 1;
int B = 2;
int C = 3;
int D = 4;
bool ret = false;

if (((A+B) && (C+D)) == true)
{
　　// (A+B)と(C+D)の値が同じであった時だけ、このシーケンスに入り、必要な処理をする
　　// ここでは、bool ret に「true」とセットしてみる例とする
　　ret = true;
}

このような条件分岐にも利用できます。

もちろん、これだけではなく、switch文等色々な用途で使うことができます。

1-2. 論理和（OR）

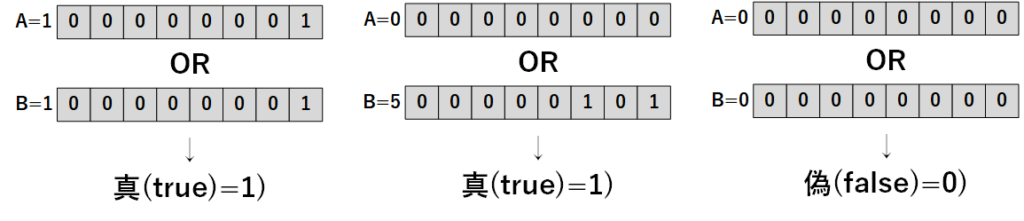
論理和は、２つビットのうち少なくとも１つが真(1)の場合に「真(true)=1」を返し、両方とも偽(0)の場合は「偽(false)=0」を返します。

論理和の記号：||
【例】A = 1、B = 1
　　　A || B = 真（true:1）　　// AもBも「0(偽)」ではないので「真」となる
【例】A = 0、B = 5
　　　A || B = 真（true:1）　　// Aは「0(偽)」だが、Bは「0(偽)」ではないので「真」となる
【例】A = 0、B = 0
　　　A || B = 偽（false:0）　 // AとBの両方が「0(偽)」なので「偽」となる

C言語ではこのような使い方をします。

int a = 5;
int b = 10;
bool ret = false;

if ((a > 0) || (b < 0))
{
　　// (a>0)aが1以上であるか、または (b<0)bが-1以下である場合に
　　// このシーケンスに入り、必要な処理をする
　　// ここでは、bool ret に「true」とセットしてみる例とする
　　ret = true;
}

これは、(a > 0)：a が 1 以上であるかどうかの判定結果と、(b < 0)：b が -1 以下であるかどうかという２つの判定結果を「OR」で比較しているもので、この式の場合、(a > 0)の判定が「真」で、(b < 0)の判定は「偽」、OR判定はどちらかが「真」であれば「真」という結果が出るので、上の if 文の条件に入ることになる。

1-3. 排他的論理和（XOR）

排他的論理和は、一見、論理和(OR)に似ていますが、少し違います。

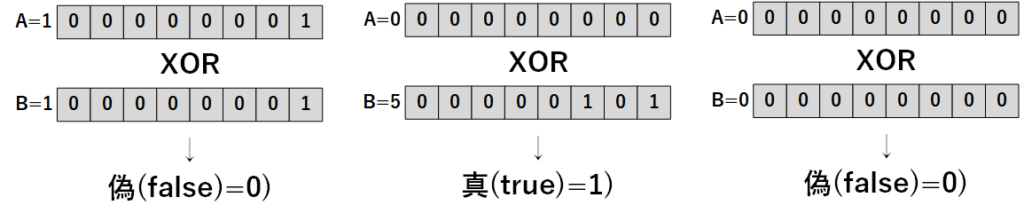
排他的論理和は、2つの条件のうち「片方だけが真の場合」に真を返し、両方が真または両方が偽の場合は偽を返す論理演算です。

論理和(OR)の場合は、「片方だけが真の場合」ではなく、「どちらか片方でも真の場合」という条件で、どちらも「真」であっても「真」という結果を返します。

それに比べて、排他的論理和(XOR)は、「どちらかだけが真である」という状態を判定します。

論理和の記号：^
【例】A = 1、B = 1
　　　A ^ B = 偽（false:0）　　// AもBも「1(真)」なので「偽」となる
【例】A = 0、B = 5
　　　A ^ B = 真（true:1）　　// Aは「0(偽)」で、Bだけが「1(真)」なので「真」となる
【例】A = 0、B = 0
　　　A ^ B = 偽（false:0）　 // AとBの両方が「0(偽)」なので「偽」となる

C言語ではこのような使い方をします。

int a = 5;
int b = 3;
bool ret = false;

if ((a ^ b) == true)
{
　　// a または b のどちらかが 1 以上の「真」である場合だけ、
　　// このシーケンスに入り、必要な処理をする
　　// ここでは、bool ret に「true」とセットしてみる例とする
　　ret = true;
}

これは、「a」は「5」が代入されているので 0 以外で「真」、「b」も「3」が代入されているので 0 以外で「真」、よって、a も b も両方ともが「真」であるため、XOR判定の結果は「偽」が返され、上の if 分の条件には 入らない ということになります。

【論理和（OR）と排他的論理和（XOR）の違い】

条件A	条件B	論理和（OR）	排他的論理和（XOR）
真	真	真	偽
真	偽	真	真
偽	真	真	真
偽	偽	偽	偽

1-4. 否定（NOT）

否定は、与えられた条件の真偽を逆転させる演算です。真の場合は偽を、偽の場合は真を返します。

論理和の記号：!
【例】A = 1
　　　!A = 偽（false:0）　 　 　 // A の「1」を否定した結果は「0(偽)」
【例】A = 0
　　　!A = 真（true:1）　　　 　 // A の「0」を否定した結果は「1(真)」
【例】A = 3、B = 0
　　　!(A + B) = 偽（false:0）　 // A+B の結果「3」を否定した結果は「0(偽)」

C言語ではこのような使い方をします。

int a = 10;
bool ret = false;

if (!(a) == true)
{
　　// a の値を否定した結果が「真」である場合だけ、
　　// このシーケンスに入り、必要な処理をする
　　// ここでは、bool ret に「true」とセットしてみる例とする
　　ret = true;
}

これは、もともと「a」には「10」のいう「真」の値が代入されており、if 文でその値を「否定」した結果が「真」である場合に ret = true; を代入する、という条件にしている。

「a」に代入された値は、否定されると「真」から「偽」に変わるので、この場合は、if 文の条件には入らないということになります。

---

2. シフト演算

シフト演算は、ビット単位での左シフト（左へのビット移動）または右シフト（右へのビット移動）を行う演算で、整数型のデータのビットパターンを変更することができます。

2-1. 左シフト

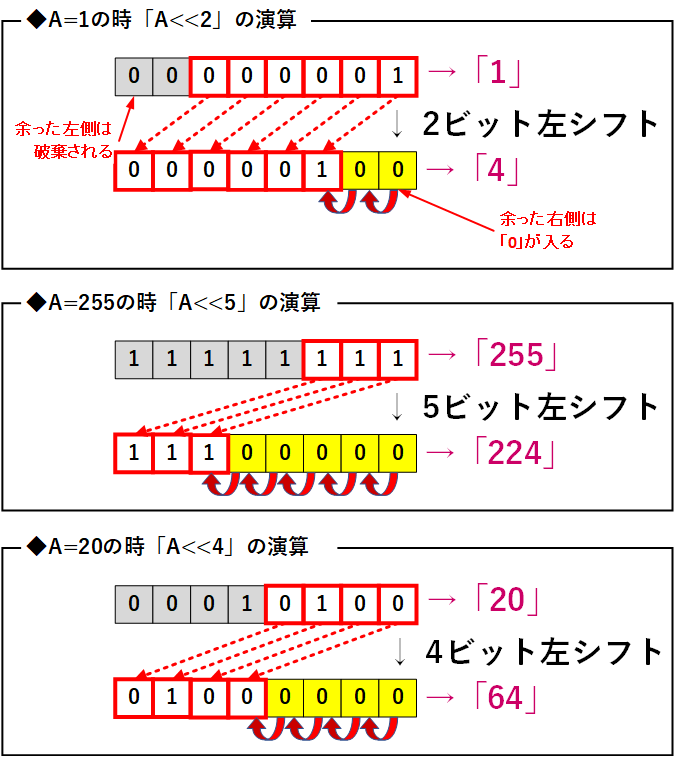
ビット列を左に指定された数だけシフトでき、シフトされた際には、右側に0が追加され、左端からあふれたビットは捨てられます。

左シフトの記号：<<
【例】A = 1、Aを 2ビット分 左シフト する
　　　A << 2 → 00000001 << 2 → 00000100（数値では 4 となる）
【例】A = 255、Aを 5ビット分 左シフト する
　　　A << 5 → 11111111 << 5 → 11100000（数値では 224 となる）

C言語ではこのような書き方をします。

int a = 20;   // 00010100 (2進数)
int shift_a;  // シフトした結果の値を入れる変数

//ここでは、2ビット左シフトさせた計算をしたい
shift_a = (a << 2);

printf("シフトした後の数値は [%d] です\n", shift_a);

00010100の値を2ビット左にシフトすると、01010000 (80) となり、この時の printf の結果は以下のように出力される

シフトした後の数値は [80] です

左シフト演算は、元の値が0・1でない限り「2のべき乗倍」するという法則があります。

プログラムで、咄嗟にべき乗計算をする必要がある時などは、効果的ですね。

2-2. 右シフト

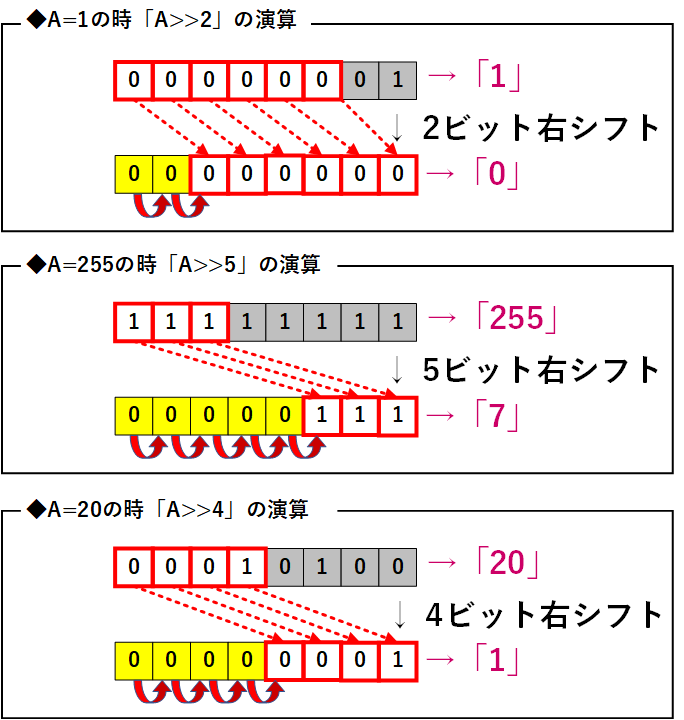
ビット列を右に指定された数だけシフトでき、シフトされた際には、左側に0が追加され、右端からあふれたビットは捨てられます。

※もっと細かい話になると、算術右シフト、論理右シフトというものがありますが、ここでは、論理右シフトとして説明します。

右シフトの記号：>>
【例】A = 1、Aを 2ビット分 右シフト する
　　　A >> 2 → 00000001 >> 2 → 00000000（全部ビットが0になってしまう、数値では 0 ）
【例】A = 255、Aを 5ビット分 右シフト する
　　　A >> 5 → 11111111 << 5 → 00000111（数値では 7 となる）

C言語ではこのような書き方をします。

int a = 20;   // 00010100 (2進数)
int shift_a;  // シフトした結果の値を入れる変数

//ここでは、2ビット右シフトさせた計算をしたい
shift_a = (a >> 2);

printf("シフトした後の数値は [%d] です\n", shift_a);

00010100の値を2ビット右にシフトすると、00000101 (5) となり、この時の printf の結果は以下のように出力される

シフトした後の数値は [5] です

右シフト演算は、左シフト時と反対に、元の値が0・1でない限り「2のべき乗で除算」するという法則があります。

ビット演算は、活用できるようになると、非常に便利です。
是非覚えてプログラミングに活用してください。

---

C言語の基礎をイメージしながら勉強できます

---